事考帮APP
让考事变得更简单










请使用微信扫描二维码,登录事考帮
 成功弹窗点击
成功弹窗点击
 失败弹窗点击
失败弹窗点击
 警告弹窗点击
警告弹窗点击
 提示弹窗点击
提示弹窗点击
A
B
x ≤ y ≤ 1.15x
C
1.15x ≤ y<1.3x
D
y ≥ 1.3x
正确答案 :D
解析
D 【解析】行程问题。由题意可知 A、B、C 三地是一个边长为 x 的等边三角形。赋值甲车速度为 1,则乙车在上坡、平路和下坡的速度分别为 0.5,1,2。
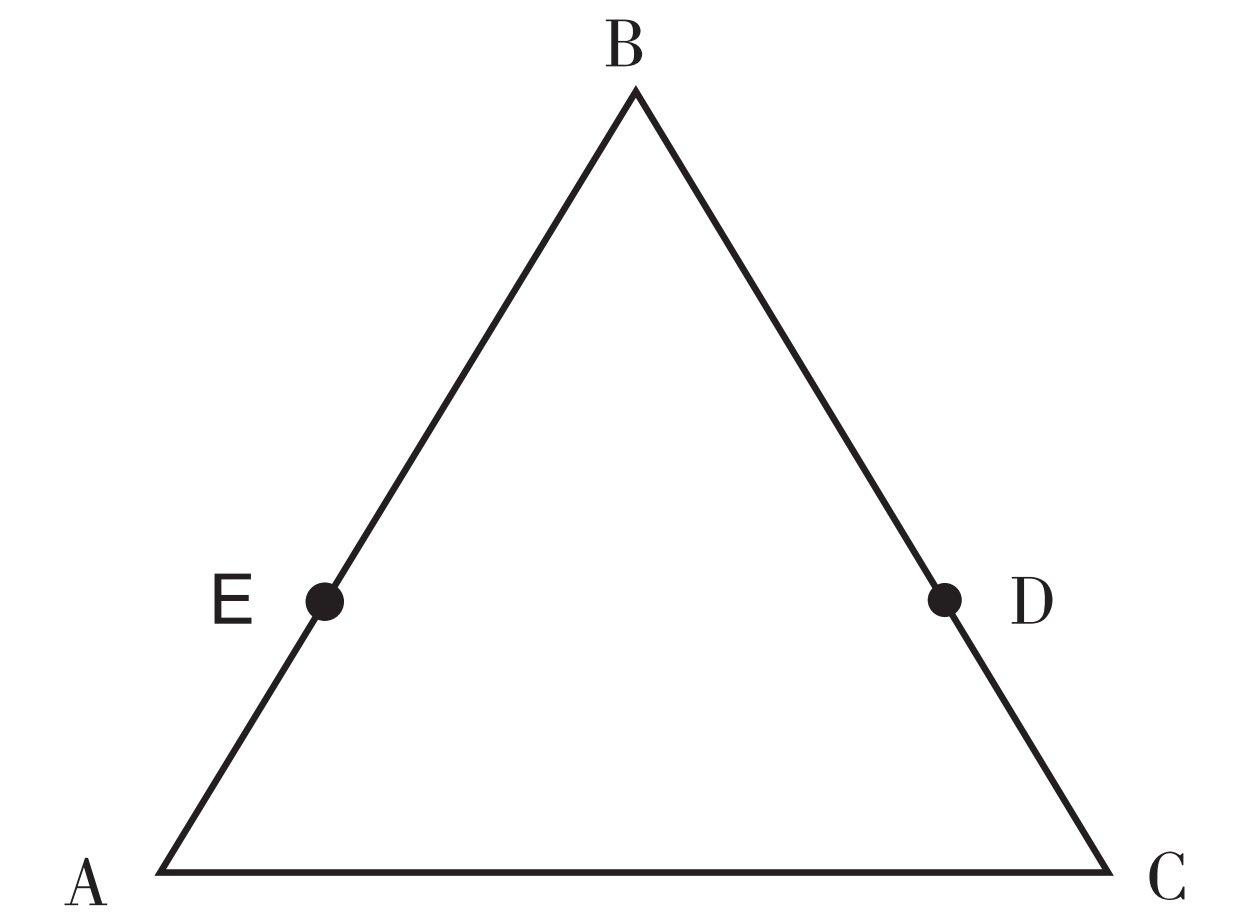
如下图,
甲从 A 到 B,乙从 A 到 C,速度相同,路程相同,则时间相同,因此第一次相遇点在BC 上的点 D 处,甲从 B 到 C,速度为 1,乙从 C 到 B,速度为 0.5,时间相同,路程与速度成正比,故相遇时甲走了 2/3x,乙走了 1/3x,即 BD=2/3x;乙从 C 到 B 速度为 0.5,则乙到达 B 点时,时间相同,甲走了 2BC=2x,即甲到了 A 点,则第二个相遇点在 AB 上的点 E 处,甲再次从 A 点出发,速度为 1,乙从 B 点到 A 点,速度为 2,时间相同,故第二次相遇时甲走了 1/3x,乙走了 2/3x,即 BE=2/3x。y=BD+BE=4/3x ≈ 1.33x。故本题答案为 D 项。
相关试题
8.关于中国历史上著名的改革,下列说法错误的是( )。
6.下列四个宣言按出现时间的先后顺序,排列正确的是( )。①《人权宣言》②《共产党宣言》③《独立宣言》④《解放黑人奴隶宣言》
把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是( )。
89.2019 年 2 季度,S 地区累计起飞架次数同比增速在以下哪个范围内( )?
2.我国脱贫攻坚取得了决定性成就,下列与之相关的说法错误的是( )。
籍势而为指的是合理利用所处环境、地位而积极践行理想信念的进取心态。根据上述定义,以下哪项属于籍势而为( )。
33 、 (单选题) 经过高尔顿、宾尼特、戈达德等人百年来的“不懈努力”,终于将智商测试 _________成一门“科学”,并得到了社会的普遍认同,于是智商测试实际上就成为又一个相对“_________”的筛选机制。它和作为主要筛选机制的现代教育相伴而行,作为“教育筛选”的辅助手段,确实有着某种程度的_________。填入横线处恰当的是:
火山爆发对于( )相当于社会变革对于( )。
交警:特警:警察
图示为中亚的地理环境要素的内在联系分析,依次填入下列空白中正确的是( )。
38.从早几年的“技工荒”,到目前劳动力市场呈现出以体力劳动为主的技工、普工同时紧俏,与此同时,不少高校毕业生仍在为一份工作发愁。这种强烈的对比,将劳动力市场的结构性供需矛盾以一种超出人们惯常认知的方式展现在世人面前。有学者认为,造成这一现象的深层次根源在于,全社会整体的择业意愿与社会需求的背离程度正在不断加深。 以下哪项如果为真,不能支持上述结论?( )
24.进入“移动互联”时代,我们获取特定知识越来越容易。以往,需要在图书馆中找寻多日的研究资料。今天,借助移动互联,借助一些搜索工具,这些知识都可以随时随地_____。今天,重要的已经不再是掌握特定知识,而是具备较高的思维水平,而是对信息的重要性做出_____,而是在各种可能的候选方案中快速做出自己的抉择。依次填入画横线部分最恰当的一项是( )。